中学受験でよく目にする旅人算。
速さの単元の応用問題の中でも王道です。
速さそのものが苦手な単元というお子さんは多いと思います。
苦手な単元の応用問題を教えるのは難しい・・・と思いがちですが、旅人算はコツさえつかめば簡単に解くことができるようになります。
今回はそんな旅人算の解き方について書いていきます。
旅人算の2地点から出発して出会う出会い算の問題の解き方とコツ
2人が別々の地点を出発して向かい合って進む旅人算の問題です。
まずは問題文の内容をしっかり理解しましょう。
それでは早速例題をみていきます。
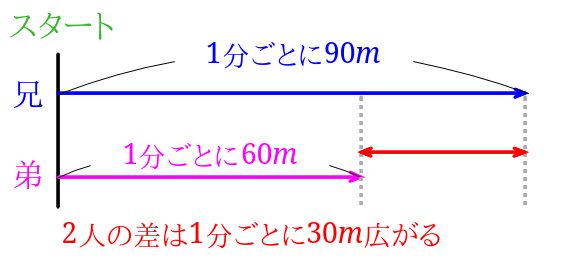
兄が\(A\)地点から\(B\)地点に向かって分速\(80m\)で、弟が\(B\)地点から\(A\)地点に向かって分速\(48m\)で同時に歩き始めました。
①2人が出会うのは歩き始めて何分後ですか。
②2人が出会うのは\(A\)地点から何\(m\)のところですか。
①を見ていきましょう。
2人が出会うまでに移動した距離の和が\(3.2km\)になりますよね。
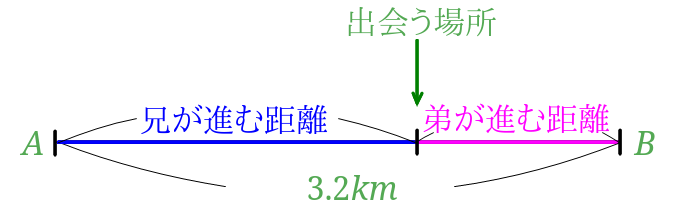
これをうまく利用するのがポイントになってきます。
兄は1分間に\(80m\)弟は1分間に\(48m\)歩くので、2人の歩いた距離の和は、1分間に\(128m\)ずつ増えるということになります。
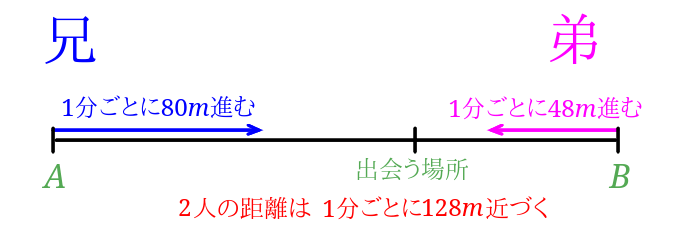
2人の歩いた距離の和が\(3.2km\)、\(3200m\)となった時に2人は出会うので、$$3200\div 128=25$$2人が出会うのは歩き始めて25分後ということが分かりました。
それでは引き続き②を解いていきましょう。
2人が会うまでの時間は①で25分と分かっているのでこれを使います。
\(A\)地点を出発して\(B\)地点に向かったのは兄なので、求める答えは兄が移動した距離と等しいことが分かります。$$80\times 25=2000$$\(A\)地点から\(2000m\)の地点で2人が出会ったことが分かりました。
姉は自転車に乗って家から公園まで分速\(175m\)の速さで、妹は公園から家まで秒速\(75m\)の速さで歩いて行きます。
2人が同時に出発して出会うのは公園から何\(m\)の地点ですか。
先ほどの例題と同じように考えると解くことができます。
2人が出会う場所やその時間がわからないので、2人の移動した距離の和を利用して答えを求めていきます。
2人が出会うまでに移動した距離の和は家から公園までの距離に等しいので、\(2500m\)と分かります。
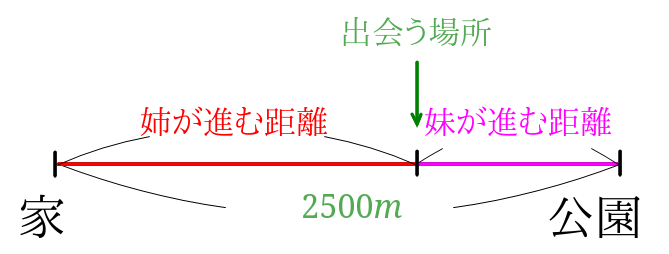
また姉が移動する距離は1分ごとに\(175m\)、妹が移動する距離は1分ごとに\(75m\)なので、1分ごとに増える2人が移動した距離の和が分かります。$$175+75=250$$姉と妹が移動した距離の和は1分ごとに\(250m\)増えることが分かりました。
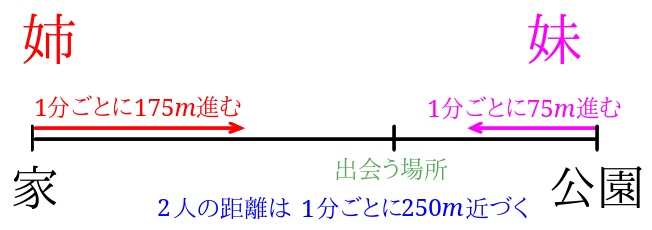
2人の移動した距離の和が、\(2500m\)になった時に2人は出会います。$$2500\div 250=10$$問題で聞かれているのは、公園から2人が出会った場所の距離にあたるので、$$75\times 10=750$$公園から\(750m\)の地点で2人が出会ったことが分かりました。
速さの公式を中心に考えていくと、距離や速さ、時間を直接求めることばかりに気が行きがちになります。
きちんと問題文を把握するのがこの、問題を解くための第1歩です。
まずはゆっくり文を読んで何をしているのかを考えるといいのではないでしょうか。
旅人算の追いかけて追いつくような追いつき算の解き方とコツ
次に「太郎君が先に家を出てその後お兄ちゃんが太郎君を追いかけました。」みたいな感じの旅人算の問題を扱います。
先程の「出会い算」との違いは進む方向が同じになるところです。
きちんと意味を考えながら例題を解いていきましょう。
姉は分速\(100m\)の速さで家から学校へ向かいました。
その2分後に弟は分速\(200m\)で家から学校へ向かいました。
①弟が姉に追いついたのは姉が家を出て何分後ですか。
②弟が姉に追いついたのは家から\(何m\)のところですか。
①からみていきましょう。
姉が家を出て2分後の姉と弟の位置関係を把握しておきましょう。
姉が家を出て2分後に進んだ道のりは、$$100m\times 2=200$$となるので、家から\(200m\)の地点に姉がいることになります。

今回の問題では姉が家を出てから2分後に弟が家を出るのですが、まずは1分ごとに2人の距離がどれだけ縮むのかを求めましょう。
1分間に姉は\(100m\)進み、1分間に弟は\(200m\)進むので、1分間に2人の距離がどれだけ縮むのかを求めると、$$200m-100m=100m$$となります。
2人の距離は弟が家を出たときには\(200m\)だったので、弟が姉に追いつくのは、$$200m\div 100=2$$となるので、弟が家を出て2分後に姉に追いつくことになります。
答えは姉が家を出てからの時間なので、\(2+2=4\)となり、求める答えは4分となります。
問題がをきちんと把握してないとつい2分と答えを書いてしまうので気を付けさせてくださいね。
それでは②にいきます。
①で姉が家を出てから4分後に弟が姉に追いつくので、姉が4分移動した地点が答えとなります。$$100m\times 4=400$$となり、答えは\(400m\)ということになります。
きちんと情報を整理する事が大切ですね。
もう1題例題をみてみましょう。
弟が家を出てから1分後に兄は自転車で家を出て、\(1500m\)地点で弟を追いこし、プールへ向かいました。
①弟が家を出て何分後に兄は弟を追いこしましたか。
②兄は時速何\(km\)の自転車に乗っていましたか。
①からみていきましょう。
弟の速さの単位が時速\(15km\)と大きく、扱いにくいので、まずは弟の速さの単位を分速○\(m\)に変えます。
すると、弟の速さは分速\(250m\)ということが分かります。
兄が弟を追い抜く地点が家から\(1500m\)の地点と分かっているので、$$1500m\div 250=6$$弟が家を出てから6分後に兄が弟を追い越すことが分かりました。
①の答えは6分後となります。
次に②をみていきます。
まず出発した時点での兄と弟の位置関係を把握しましょう。
弟が家を出て1分後に兄が家を出るので、$$250m\times 1=250$$となり、弟は家から\(250m\)のところにいることになります。
また兄が弟を追い抜くのは兄が家を出てから5分後ということになります。
と、言うことは、\(250m\)の距離を5分かけて追いつくということは、1分あたりに何\(m\)差が縮まるのかが分かります。$$250\div 5=50$$1分間に\(50m\)差が縮まるということは兄は弟よりも分速\(50m\)速いということになります。$$250+50=300$$となり、兄の
速さは分速\(300m\)ということになります
答えは時速\(km\)を聞かれているので、分速\(300m\)から時速○\(km\)に単位変換をして、時速\(18km\)となります。
求めるものが1つではないので少し難しく感じるかもしれません。
そうはいっても順番に求めていけばきちんと解けます。
焦らずゆっくり解きたいですね。
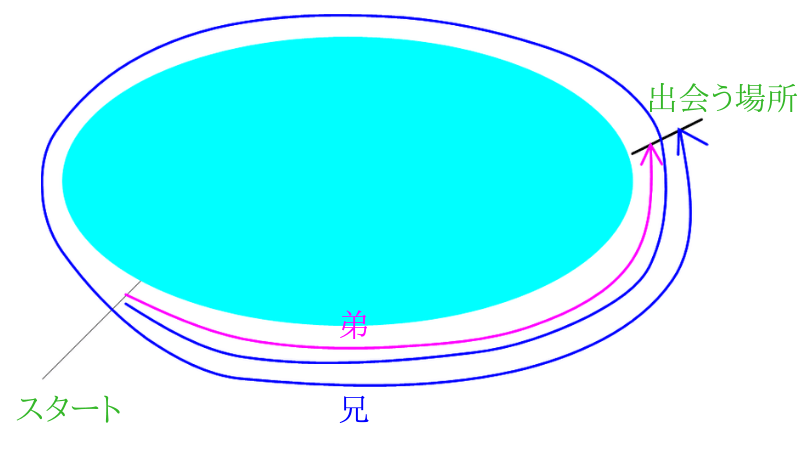
旅人算の池の周りを反対方向にまわる出会い算の解き方とコツ
池の周りを反対向きにまわる出会い算になります。
解法のポイントはその問題の捉え方です。
捉え方を間違えると難問化してしまうので、そうなってしまわないようにしっかり問題を的確にとらえていきましょう。
それでは例題を使って考えていきます。
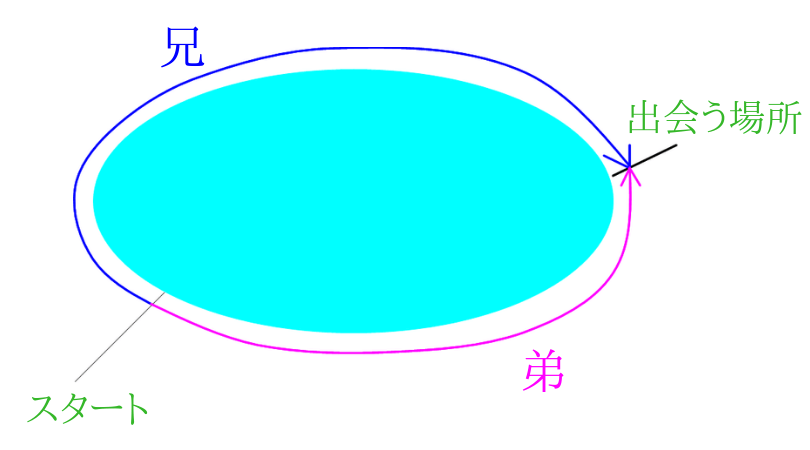
その池の\(A\)地点から兄は分速\(80m\)で時計まわりに、弟は分速\(70m\)で反時計まわりに同時に歩き始めたとき、2人が出会うのは歩き始めて何分後になりますか。
兄と弟が池の周りを反対方向にまわって、出会うまでの時間を求める問題です。
この問題の難しさは、いつ、どこで出会ったのかが分からないというところです。
ここをうまくクリアしないことには答えに行きつくことができません。
ポイントは、兄と弟のそれぞれの移動距離を考えないことです。
2人が出会うまでにお兄ちゃんと弟君が移動したそれぞれの距離をいきなり求めることはできません。
ちょっと見方を変えることが大事です。
兄と弟が出会うまでに移動した2人の距離の合計を考えていきます。
2人が出発して出会うまでに移動したそれぞれの距離の和は、池1周分の\(1200m\)です。
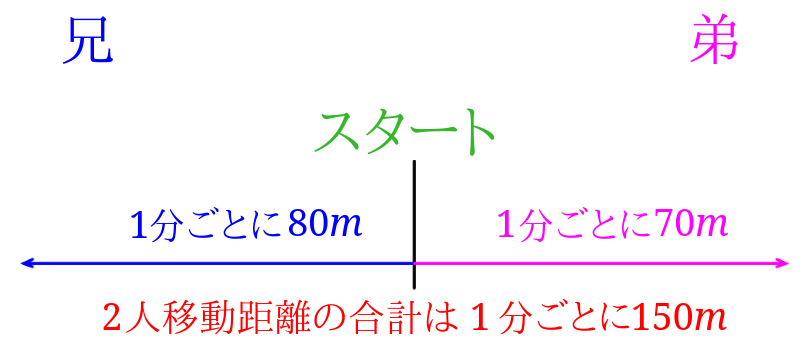
 また2人の移動した距離の合計は1分ごとに\(150m\)ずつ増えていきます。
また2人の移動した距離の合計は1分ごとに\(150m\)ずつ増えていきます。
 2人の移動した距離の合計が\(1200m\)になった時に出会うので、2人が出会うまでにかかる時間は、$$1200\div 150=8$$2人が出会うまでにかかる時間は8分となります。
2人の移動した距離の合計が\(1200m\)になった時に出会うので、2人が出会うまでにかかる時間は、$$1200\div 150=8$$2人が出会うまでにかかる時間は8分となります。
答えは2人が歩き始めて8分後ということになります。
動くものが2つの時は個々で移動した距離は求めにくくても、その2つの移動した距離の和は求めやすいことが多いです。
今回の池の問題のように反対方向に同じ地点を出て出会うまでというような場合は、2つの動くものが移動した距離の和=池の周りの長さということが分かれば解けるようになります。
速さの理解というよりはまずはその問題文中で起こる現象の理解が先に来ると思います。
この辺りは速さの問題というよりは物事のとらえ方に近いです。
速さの問題の解き方とは独立した全く別のものとしてとらえて教えてあげるほうが分かりやすいかもしれませんね。
次に必要なるのは今回の例題で必要になるのは1分間に2人が移動した距離の合計です。
一般的に言うと、ある単位量当たりに2つのものが移動した距離の和という感じでしょうか。
移動する方向が逆になっている問題では基本的にそれは速さの和になります。
学校や塾によっては暗記するように教えられていることもありますが、どういう現象なのかを考えることができれば、自然と速さの和を使うことになります。
単に「反対向きに移動するときには速さの和を使う」というような感じではあまりとらえさせたくありませんね。
難しいと言われる速さの文章題はその文章題が言っていることをどのように解釈するかにかかっています。
その問題文から分かることを一緒に考えてあげるのがややこしい文章問題でも解けるようになる近道かもしれませんね。
もう1題例題をやってみましょう。
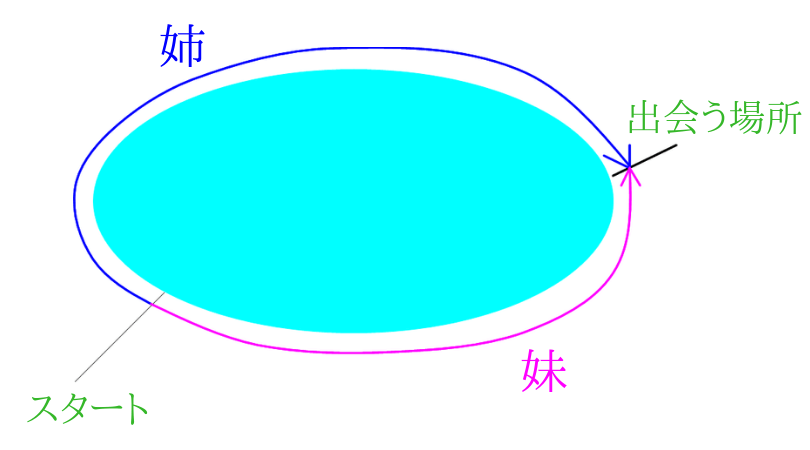
2人が出会ったとき、姉はスタート地点から何\(km\)進んだことになりますか。
先ほどの例題と似ていますが、聞かれていることが変わりましたね。
基本的な解き方は変わりません。
先ほどと同じように2人が同じ地点から、同時に、反対方向にスタートして出会うという問題です。
今回の問題でも2人の移動した距離の和がポイントになります。
出会うまでに2人が移動した距離の和は\(24km\)ということが最初に分かります。
次に2人の1分間に移動した距離の和を考えます。[1] … Continue reading
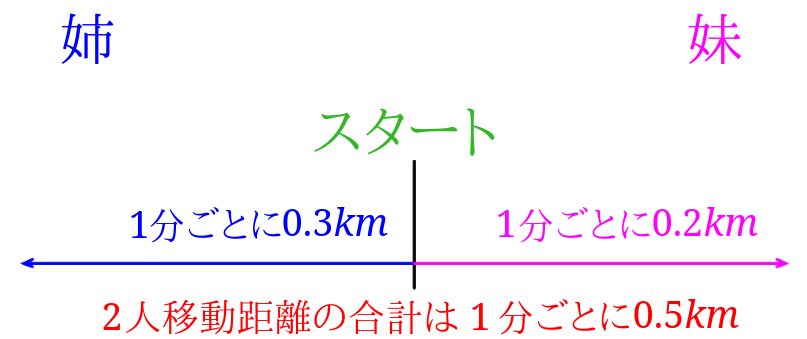
姉の時速\(18km\)を分速に単位を変えてみましょう。$$18\div 60=0.3$$姉の速さは分速\(0.3km\)ということになります。
ということは、姉と妹が1分間に移動した距離の和は、$$0.3+0.2=0.5$$姉と妹が1分間に移動する距離は\(0.5km\)と分かりました。
2人が出会うまでにかかる時間は、$$24\div 0.5=48$$出会うまでに48分かかることが分かりました。
問題で聞かれているのは姉がスタート地点からすすんだ距離なので、$$0.3\times 48=14.4$$答えは\(14.4km\)ということになります。
妹の速さを時速にしたときの求め方
この問題では分速のほうがお子さんがとらえやすいと思いますが、時速に単位を合わせたときの解き方も解説しておきますね。
妹の速さを時速に単位変換すると、$$0.2\times 60=12$$妹の速さは時速\(12km\)ということが分かりました。
2人が1時間に進む距離は、$$18+12=30$$\(30km\)だということが分かりました。
出会うまでにかかった時間は、$$24\div 30=0.8$$姉がスタート地点から妹と出会うまでに進んだ距離は、$$18\times 0.8=14.4$$答えは\(14.4km\)となります。
時速に合わせても問題の解き方は全く同じです。
時間を基準にするのか分を基準にするのかの差です。
扱いやすい単位をうまく設定することで、計算が楽になるためちょうどいい単位に合わせてあげるといいですね。
旅人算の池の周りを同じ方向にまわる追い越し算の解き方とコツ
池の周りを同じ方向にまわる追い越し算の問題です。
まずは問題の理解が大事になるので理解しながらすすめていきましょう。
初めて兄が弟を追いこすのは2人が出発して何分後になりますか。
兄と弟の進んだ距離を考えて解こうとするととんでもなくややこしくなってしまいます。
この問題は兄と弟が同時に同じ方向に出発して兄が弟に追いつくまでの時間を求める問題です。
そのまま頭の中で兄と弟を歩かせてみると…どうすれば追いつくのかイメージが作りにくいですよね。
という訳でちょっと視点を変えて追いついてしまった時の兄と弟の歩いた距離を考えてみましょう。
兄が弟に追いつくということは、兄のほうがたくさん歩いたことは分かりますよね。
兄は弟よりもどれだけ長く歩いたのでしょうか。
ここが1番のポイントです。
追いつくというのは少し見方を変えると、「兄のほうが池を1周多くまわった」ということですね。
ということは、兄が歩いた距離は弟が歩いた距離よりも、池1周分多いということが分かります。
つまり、この問題では兄のほうが弟よりも\(1800m\)長く歩いたということになります。
また兄の歩く速さは分速\(90m\)、弟が歩く速さは分速\(60m\)です。
2人が1分歩くごとに、\(30m\)兄のほうが多く歩くことになります。[2]差が付くと言うことですね。
先程兄のほうが\(1800m\)多く歩くことが、分かりましたよね。
兄は1分ごとに\(30m\)弟よりも長い距離を歩いたことになります。
つまり、兄が弟に追いついた時間は、$$1800\div 30=60$$出発して兄が弟に追いつくのは出発して60分後ということがわかりました。
その湖の周りを兄は時速\(7.2km\)で走り、妹は秒速\(5m\)の自転車に乗りました。
2人は同時に同じ方向へ出発します。
妹が兄を初めて追いこしたとき、妹は何\(m\)自転車に乗ったことになりますか。
まずは兄の速さ時速\(7.2km\)を、秒速○\(m\)の形にすると、秒速\(2m\)。
同じ方向に進んで妹が兄を追いこすときを求めます。
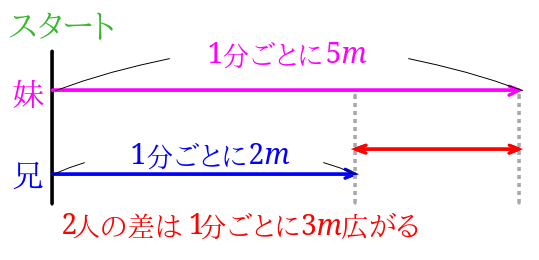
妹が兄の進んだ距離よりも湖1周分の長さ、\(3600m\)長く進んだ時に兄を追い越します。

兄は秒速\(2m\)、妹は秒速\(5m\)なので、2人の距離は1分ごとに\(3m\)ひらくことになります。
その差が、\(3600m\)になった時に妹が兄を追い越すので、追い越す時間を求めると、$$3600\div 3=1200$$妹が兄を追いこすまでの時間はスタートしてから、1200秒後ということになります。
求める答えは妹が自転車に乗っていた距離なので、$$5\times 1200=6000$$妹が自転車にのっていた距離は\(6000m\)ということになります。
まとめ
旅人算の基本的な4種類の問題を扱いました。
これらの問題が旅人算の基礎になります。
また、流水算という特殊算を解くときも必要になる考え方です。
きちんと意味を押さえて解けるようにしましょう。
【関連記事はこちら】
・旅人算の練習問題と解説




